L'affinità è una trasformazione lineare che conserva il parallelismo fra rette, il rapporto fra segmenti corrispondenti, il rapporto fra le aree di figure corrispondenti, ma non conserva la lunghezza dei segmenti e l'ampiezza degli angoli.
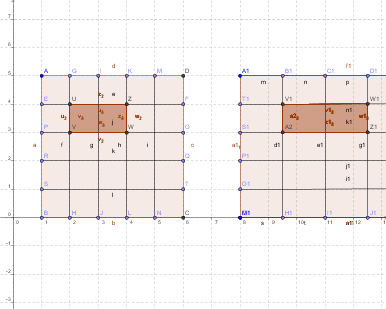
Nella figura 42 è disegnata una figura F ricoperta da un reticolato R a maglie quadrate, nella figura 43 è rappresentato un altro reticolato R' formato dallo stesso numero di maglie rettangolari.

A ogni quadrato del reticolato R si può far corrispondere un ben determinato rettangolo del reticolato R1.
A ogni punto di un quadrato del reticolato R si può far corrispondere un ben determinato punto del rettangolo corrispondente del reticolato R1 e viceversa: viene così stabilita una corrispondenza biunivoca tra i punti dei due reticolati. Riproduciamo ora sul reticolato R1 la figura F disegnata sul reticolato R. Poiché le maglie dei due reticolati (quadrati e rettangoli) non sono simili la figura F1 ottenuta sul reticolato R1 non è simile alla figura F del reticolato R. Le due figure F ed F1 si dicono figuri affini e la trasformazione che fa corrispondere alla figura F con la figura F1 si dice affinità.
Confrontando la figura F con la figura F1 possiamo rilevare che:
€ alla retta r corrisponde la retta r';
€ ai segmenti paralleli AC e BD corrispondono i segmenti paralleli A'C' e B'D';
€ il rapporto tra i due segmenti paralleli BD e AH è BD/AH = 1/3 e il rapporto tra i segmenti corrispondenti (anch'essi paralleli) è B'D'/A'H' = 1/3.
Quindi il rapporto tra i due segmenti della figura F appartenenti a rette parallele (o alla stessa retta) è uguale al rapporto tra i due segmenti corrispondenti della figura F'.
Consideriamo ora il rettangolo e il parallelogrammo della figura 44, il rettangolo e il parallelogrammo corrispondenti della figura 45. Per confrontare le loro aree indichiamo:
€ nella figura 44 con R l'aria del rettangolo e con P l'area del parallelogrammo;
€ nella figura 45 con R' l'area del rettangolo e con P ' l'area del parallelogrammo corrispondenti.
Nella figura 44 l'area R del rettangolo e l'area P del parallelogrammo coprono rispettivamente 2 o 6 maglie. Anche nella figura 45 l'area R' del rettangolo e l'area P 'del parallelogrammo coprono rispettivamente 2 o 6 maglie.