LE TRASFORMAZIONI NON ISOMETRICHE
LA TOPOLOGIA
Se disegniamo delle figure su un sottile foglio di gomma e poi lo deformiamo, tirandolo con forza lungo il suo contorno, otteniamo una trasformazione geometrica delle figure che dopo la deformazione risultano assai diverse, poiché hanno perso in modo evidente la forma e le dimensioni iniziali.
Anche se la trasformazione è notevole, nelle figure trasformate restano tuttavia inalterate alcune caratteristiche delle figure iniziali.
Trasformazioni geometriche di questo genere si dicono trasformazioni topologiche o semplicemente topologie.
La topologia si occupa delle figure che cambiano grandezza e forma e ha per proprietà invarianti:
Il tipo di linea.
La continuità della linea.
L'appartenenza o la non appartenenza di un punto a una linea.
La collocazione di un punto all'interno o all'esterno di una linea chiusa.
L'ordine con cui sono disposti i punti di una data linea.
Due figure ottenute l'una dall'altra per trasformazione topologica sono in corrispondenza biunivoca.
Due o più linee si dicono topologicamente equivalenti se si possono ottenere l'una dall'altra mediante trasformazioni topologiche.

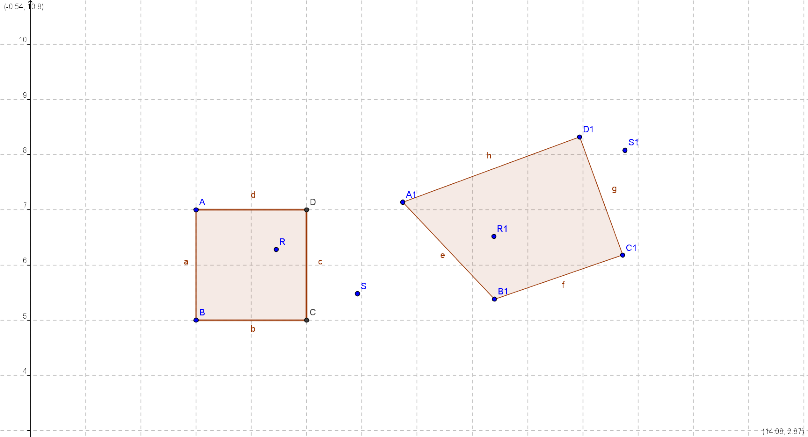
Una linea chiusa semplice rimane una linea chiusa semplice e il punto R, interno alla linea, rimane all'interno della linea.
Un quadrato è topologicamente equivalente a un triangolo o a un cerchio, ma non a un segmento o a una retta in quanto non è possibile deformare il piano su cui giace il quadrato in modo da ottenere una retta.
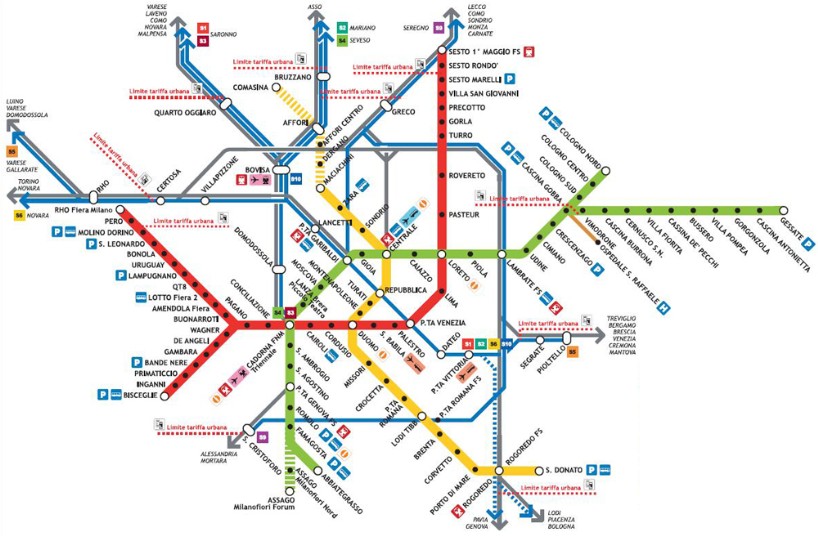
Le cartine che descrivono i percorsi delle linee metropolitane delle città sono esempi di trasformazioni topologiche.