LE CONICHE CON IL SOFTWARE OPEN SOURCE GEOGEBRA
PREMESSA
L'importante argomento delle coniche rappresenta, certamente, una delle parti più interessanti e stimolanti della matematica. Si tratta, però, di saperla rendere tale, sollecitando la naturale curiosità del giovane e attivando un processo dinamico di insegnamento-apprendimento, incentrato sul metodo della scoperta. L’itinerario didattico dovrebbe avere un andamento “circolare”, che partendo dalla impostazione dei problemi geometrici proposti, conduce alla loro trasposizione algebrica, all’analisi e alla valutazione dei risultati trovati, per poi ripartire con nuovi problemi.
In questo processo diventa particolarmente utile poter disporre del programma Geogebra, moderno ed efficace ausilio che integra questo corso di matematica.
In proposito, per quanto riguarda Geogebra, se ne consiglia l’impiego in modo intensivo, ma senza che ciò stravolga il lavoro dello studente, in classe o a casa. Il giovane, di fronte a un problema, deve applicarsi e cercare di risolverlo con i tradizionali mezzi a disposizione; solo in sede di verifica farà riferimento a Geogebra, per visualizzare dati e risultati al computer, e per controllare l’esattezza dei grafici e dei calcoli svolti sul quaderno.
In taluni casi particolari (come, ad esempio, nello studio delle equazioni o delle disequazioni), può essere opportuno operare direttamente al computer, sfruttando le potenzialità del software, che consente la contemporanea visualizzazione di numerosi diagrammi e i relativi andamenti. Al contrario, un insegnamento che prevede eccessivi appesantimenti di calcoli, lunghe e noiose dimostrazioni letterali, esercizi e problemi meccanici e ripetitivi, non aiuta il giovane a entrare “in sintonia” con i contenuti della geometria analitica.
OBIETTIVI
Acquisire la capacità di tradurre problemi in forma algebrica;
Assimilare il concetto di “luogo geometrico dei punti”;
Saper riconoscere, interpretare e costruire relazioni e funzioni quadratiche;
Sviluppare l’intuizione geometrica nel piano e nello spazio cartesiano;
Discutere equazioni parametriche con metodo grafico.
CONTENUTI
Introduzione alle coniche;
Parabola;
Circonferenza;
Ellisse;
Iperbole;
Discussione dei problemi geometrici.
INTRODUZIONE ALLE CONICHE.
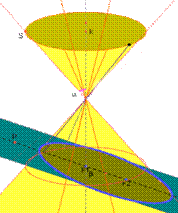
Con il termine conica, si indica una curva ottenuta sezionando, mediante un piano, una superficie conica indefinita a due falde.
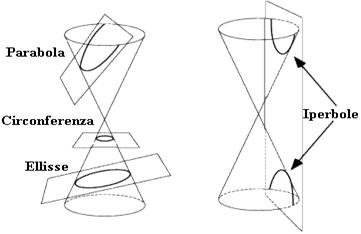
Al variare dell’ampiezza dell’angolo ß, formato dall’asse della superficie conica con il piano secante, si possono verificare quattro casi:
- Se β = 90°, la sezione è una circonferenza.
- Se α < β < 90°, la sezione è una ellisse.
- Se β = α, la sezione è una parabola.
- Se 0° ≤ β < α, la sezione è una iperbole.


LA STORIA
Lo studio delle coniche si è evoluto nel corso di diversi secoli.
Per quanto si sa, le sue le origini risalgono a Menecmo (350 a.C.) discepolo di Eudosso, che scoprì le sezioni coniche nel tentativo di risolvere il problema della duplicazione del cubo, o problema di Delo, Anche Euclide (360-300 a.C.) si interessò alle coniche sulle quali scrisse ben 4 libri andati poi perduti, la trattazione fu poi completata, dal punto di vista teorico, negli otto libri 'Le coniche' da Apolonnio (200 a.C.). Si dice che sia stato Apollonio, tra l'altro, ad aver introdotto i nomi "ellisse", "parabola", e "iperbole". Tali nomi traggono origine dal confronto di due grandezze caratteristiche di ciascuna curva. Ellisse vuol dire mancanza, iperbole significa "andare oltre", e parabola, "mettere accanto".
Pur interessante dal punto di vista matematico, lo studio delle coniche aveva scarsi interessi pratici e venne abbandonato per diversi anni. Solo dopo circa 1800 anni lo studio di Apollonio poté fare passi avanti. Questo fu dovuto essenzialmente all'introduzione dei nuovi metodi matematici basati sulle coordinate cartesiane, ma anche al sorgere di un nuovo interesse scientifico. Da segnalare nell'ordine Galileo (moto di un proiettile) Cartesio, Keplero, Pascal, ed infine Newton che utilizzarono lo studio delle coniche applicato a scoperte scientifiche.
LE CONICHE COME LUOGHI GEOMETRICI DI PUNTI DEL PIANO
Le coniche sono anche definite come luoghi geometrici di punti del piano che godono di una determinata proprietà caratteristica.
LA PARABOLA
Si chiama parabola il luogo geometrico dei punti del piano che sono equidistanti da un punto fisso F, detto fuoco, e da una retta fissa d, denominata direttrice.
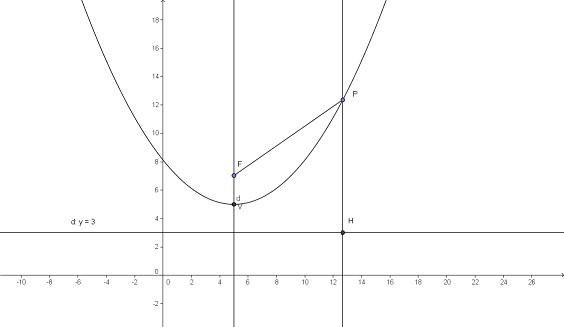
LA CIRCONFERENZA
Si chiama circonferenza il luogo geometrico dei punti del piano che sono equidistanti da un punto fisso C, detto centro. Questa distanza costante tra il generico punto P e il centro è denominato raggio, e la sua misura si indica con r.

L'ELLISSE
Si chiama ellisse il luogo geometrico dei punti del piano tali che è costante la somma delle loro distanze da due punti fissi, F1 ed F2, detti fuochi.

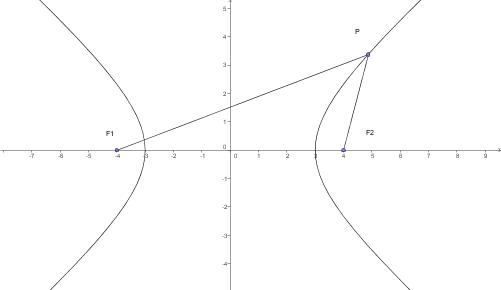
Si chiama iperbole il luogo geometrico dei punti del piano, tali che è costante la differenza delle loro distanze da due punti fissi, F1 ed F2, detti fuochi.