Bisettrice di un angolo.
La bisettrice di un angolo è l'asse di simmetria dell'angolo stesso.

Triangolo isoscele.
In un triangolo isoscele l'altezza relativa alla base equivale all'asse di simmetria del triangolo stesso.

Triangolo equilatero.
In un triangolo equilatero le altezze, le mediane, le bisettrici e gli assi equivalgono ai tre assi di simmetria. Il punto d' intersezione di questi assi si chiama centro di simmetria.

Quadrato.
In un quadrato gli assi di simmetria corrispondono alle diagonali di quest'ultimo e alle rette parallele, passanti per i punti medi dei suoi lati, ai suoi lati.

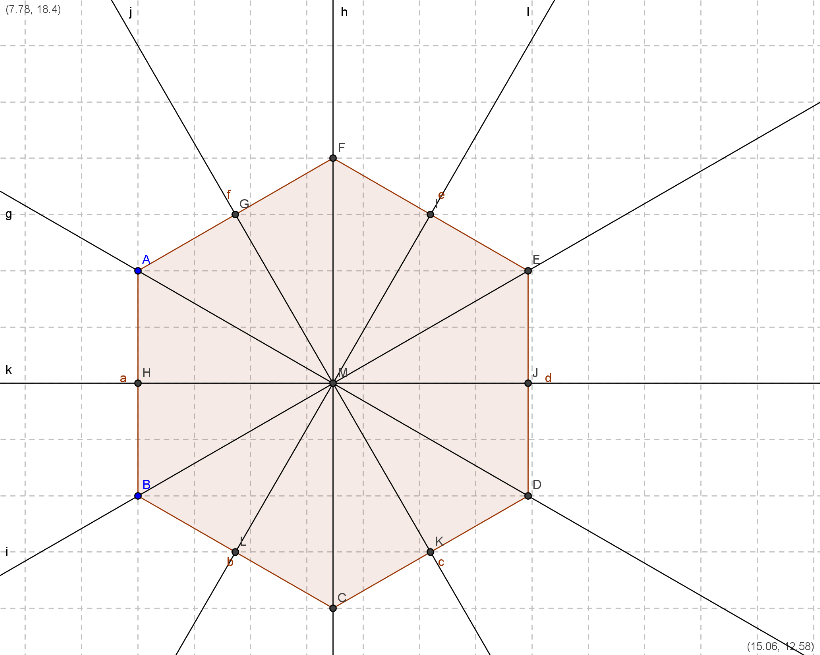
Poligoni regolari.
I poligoni regolari hanno tanti assi di simmetria quanti sono i loro lati.
Cerchio.
In un cerchio qualunque retta passante per il centro della circonferenza rappresenta un asse di simmetria. Pertanto la circonferenza ha infiniti assi di simmetria.

Il parallelogramma.
Nel parallelogramma non ci sono assi di simmetria, comunque possiamo lo stesso trovare il centro di simmetria che è il punto in cui le diagonali si incontrano.

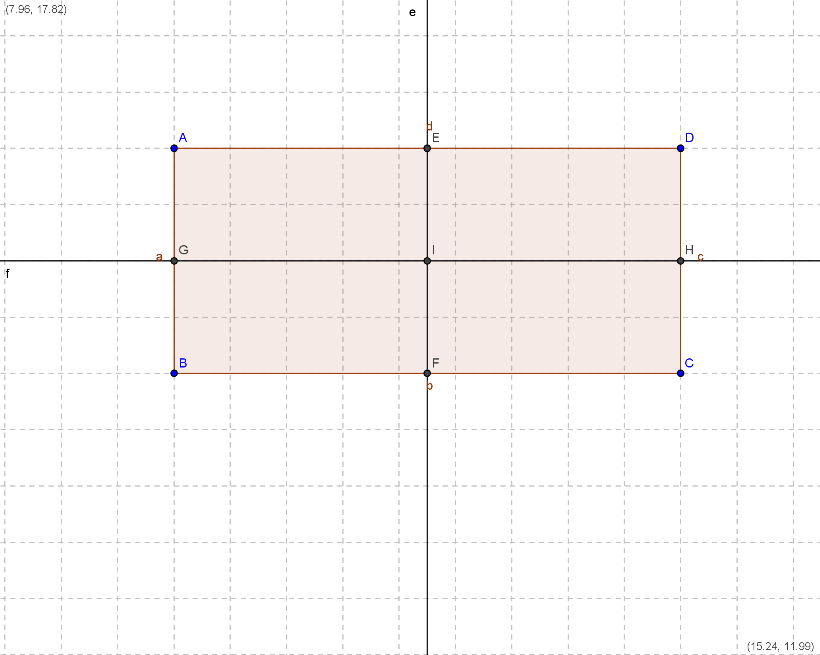
Rettangolo.
Gli assi di simmetria in un rettangolo corrispondono alle rette parallele, passanti per i punti medi dei suoi lati, ai suoi lati.
Rombo.
In un rombo gli assi di simmetria corrispondono alle sue diagonali.

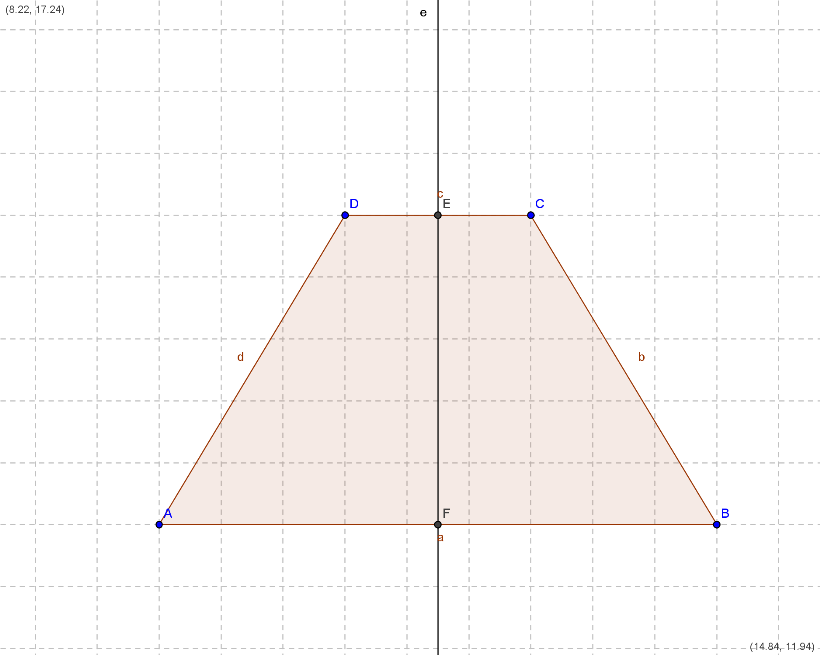
Trapezio isoscele.
In un trapezio isoscele la retta perpendicolare al punto medio delle due basi corrisponde all'asse di simmetria dello stesso trapezio.